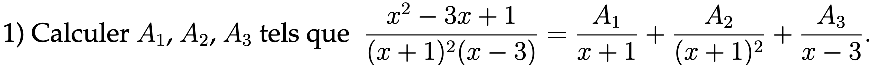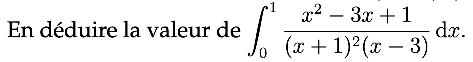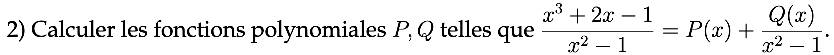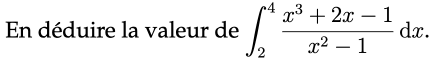cours/Exercices maths perso 2022-10-26.md

#s/maths

L2 maths algebre linéaire TD2

Exercice 6

u = (1; -1; 2; 3) et v = (1; 2; -1; 4)

Trouver des conditions nécessaires suffisantes sur x, y, z, t pour que (x; y; z; t) \in \mathrm{Vect}(u; v)

\begin{pmatrix}x \\ y \\ z \\ t \end{pmatrix} = \lambda \begin{pmatrix}1\\-1\\2\\3\end{pmatrix} + \mu \begin{pmatrix}1\\2\\-1\\4\end{pmatrix}

\begin{align}
\begin{cases}
x = \lambda + \mu \\
y = 2\mu - \lambda \\
z = 2\lambda - \mu \\
t = 3\lambda + 4\mu
\end{cases} &\iff
\begin{cases}
\mu = x - \lambda \\
\lambda = -y+2\mu \\
z = 2\lambda - \mu \\
t = 3\lambda + 4\mu \\
\end{cases} \\
&\iff 
\begin{cases}
\mu = x - y + 2\mu \\
\lambda = -y + 2\mu \\
z = 2\lambda - \mu \\
t = 3\lambda + 4\mu 
\end{cases} \\
&\iff
\begin{cases}
\mu = \frac{1}{3} x - \frac{1}{3} y \\
\lambda = -y + \frac{2}{3} x - \frac{2}{3} y \\
z = 2\lambda - \mu \\
t = 3\lambda + 4\mu
\end{cases} \\
&\iff
\begin{cases}
\mu = \frac{1}{3} x - \frac{1}{3} x \\
\lambda = - \frac{5}{3} y + \frac{2}{3} x \\
z = 2\lambda - \mu \\
t = 3\lambda + 4\mu
\end{cases} \\
&\iff
\begin{cases}
\mu = \frac{1}{3} x - \frac{1}{3} y \\
\lambda = - \frac{5}{3} y + \frac{2}{3} x \\
z = - \frac{10}{3} y + \frac{4}{3} x - \frac{1}{3} x - \frac{1}{3} y \\
t = 3=l + 4\mu
\end{cases} \\
&\iff 
\begin{cases}
\mu = \frac{1}{3} x - \frac{1}{3}y \\
\lambda = -\frac{5}{3}y + \frac{2}{3}x \\
z = x - \frac{11}{3}y \\
t = -5y + 2x + \frac{4}{3} x - \frac{4}{3}y
\end{cases} \\
&\iff 
\begin{cases}
\mu = \frac{1}{3}x - \frac{1}{3}y \\
\lambda = -\frac{5}{3} y + \frac{2}{3} x \\
z = x - \frac{11}{3}y \\
t = -\frac{19}{3}y + \frac{10}{3}x
\end{cases} \\
&\iff 
\begin{cases}
x = \lambda + \mu \\
y = 2\mu - \lambda \\
z = x - \frac{11}{3} y \\
t = \frac{10}{3}x - \frac{19}{3}y
\end{cases}
\end{align}

Si on fixe une valeur pour x, on sait que \lambda = x - \mu, donc : y = 2\mu - x - \mu \iff y = \mu - x donc y ne dépend que de \mu et de la valeur fixée de x. Alors, si \mu est fixé (pour que y soit fixé), on peut toujours trouver une valeur de \lambda telle que x = \lambda + \mu. Donc, x et y sont indépendants. On a alors :

\begin{pmatrix}x\\y\\z\\t\end{pmatrix} \in \mathrm{Vect}(u;v) \iff \begin{cases} z = x - \frac{11}{3}y\\ t = \frac{10}{3}x - \frac{19}{3} \end{cases} \text{ avec } (x; y; z; t) \in \mathbb{R}^{4}

Soit :

\mathrm{Vect}(u; v) = \left\{ \begin{pmatrix}x\\y\\x- \frac{11}{3}y\\ \frac{10}{3}x - \frac{19}{3}y\end{pmatrix} \in \mathbb{R}^{4} \right\}

L2 maths analyse TD2

Exercice 3

1)

!

\displaystyle\frac{x^{2} - 3x + 1}{(x+1)^{2}(x-3)} = \frac{A_{1}}{x+1} + \frac{A_{2}}{(x+1)^{2}} + \frac{A_{3}}{x-3}

\displaystyle \frac{x^{2} - 3x + 1}{(x+1)^{2}} = \frac{A_{1}(x-3)}{x+1} + \frac{A_{2}(x-3)}{(x+1)^{2}} + A_{3} si on pose x = 3, on a \boxed{A_{3} = \dfrac{1}{16}}

\displaystyle \frac{x^{2} - 3x + 1}{x-3} = A_{1}(x+1) + A_{2} + \frac{A_{3}(x+1)^{2}}{x-3} si on pose x = -1, on a \boxed{A_{2} = - \dfrac{5}{4}}

si on pose x = 0, on obtient :

\begin{align}
-\frac{1}{3} = A_{1} + A_{2} - \frac{1}{3}A_{3} &\iff -\frac{1}{3} = A_{1} - \frac{5}{4} - \frac{1}{3} \times \frac{1}{16}\\
&\iff A_{1} = \frac{5}{4} + \frac{1}{3}\times \frac{1}{6} - \frac{1}{3} \\
&\iff A_{1} = \frac{35}{2^{2}\times 3^{2}} \\
&\iff A_{1} = \frac{35}{36} \\
\end{align}

Donc, on a : \displaystyle\frac{x^{2}-3x+1}{(x+1)^{2}(x-3)} = \frac{35}{36(x+1)} - \frac{5}{4(x+1)^{2}} + \frac{1}{16(x-3)}

!

\begin{align}
\int_{0}^{1} \frac{x^{2}-3x+1}{(x+1)^{2}(x-3)} \, dx &= \frac{35}{36} \int_{0}^{1} \frac{1}{x+1} \, dx + \frac{5}{4} \int_{0}^{1} - \frac{1}{(x+1)^{2}} \, dx + \frac{1}{16} \int_{0}^{1} \frac{1}{x-3} \, dx \\
&= \frac{35}{36} \left[  \ln (|x+1|) \right]_{0}^{1} + \frac{5}{4} \left[ \frac{1}{x+1} \right]_{0}^{1} + \frac{1}{16} \left[ \ln(|x-3) \right]_{0}^{1} \\
&= \frac{35\ln(2)}{36} - \frac{1}{2}\times \frac{5}{4} + \frac{\ln 2 - \ln 3}{16} \\
&= \frac{35 \ln 2}{36} + \frac{\ln 2 - \ln 3}{16} - \frac{5}{8}
\end{align}

2)

!

\displaystyle \frac{x^{3}+2x-1}{x^{2} - 1} = P(x) + \frac{Q(x)}{x^{2}-1}

!Exercices evelyne 2022-10-26 2022-10-29 18.17.44.excalidraw

Donc : \displaystyle \frac{x^{3} + 2x - 1}{x^{2} - 1} = x + \frac{3x-1}{x^{2}-1}

!

\begin{align}
\int_{2}^{4} \frac{x^{3}+2x-1}{x^{2}-1} \, dx &= \int_{2}^{4} x \, dx + \int_{2}^{4} \frac{3x}{x^{2}-1} \, dx - \int_{2}^{4} \frac{1}{x^{2}-1} \, dx \\
&= \int_{2}^{4} x \, dx + \frac{3}{2} \int_{2}^{4} \frac{2x}{x^{2}-1} \, dx + \int_{2}^{4} \frac{1}{1 - x^{2}} \, dx \\
&= \left[ \frac{1}{2}x^{2} \right]_{2}^{4} + \frac{3}{2}\left[ \ln \left| x^{2}-1 \right|  \right]_{2}^{4} + \left[ \arg \mathrm{th} (x) \right]_{2}^{4} \\
&= 6 +  \frac{3}{2} \ln (5) + \arg \mathrm{th}(4) - \arg \mathrm{th}(2)
\end{align}